1편에 이어 작성합니다. 아래 링크를 남겨두었으니 1편을 보고 오시는 것을 추천드립니다!
https://chlduswns99.tistory.com/56
[논문리뷰]Transformer: Attention Is All You Need [1]
이번 논문은 그 유명한 Transformer입니다. Transformer는 기존의 RNN, CNN 기반 모델들에서 벗어나 오직 Attention 기법만을 이용해 설계했습니다. 현재 GPT, BERT 같은 널리 쓰이는 모델의 근간이 되는 아키
chlduswns99.tistory.com
이해를 돕기 위해 이미지를 다시 불러오겠습니다.
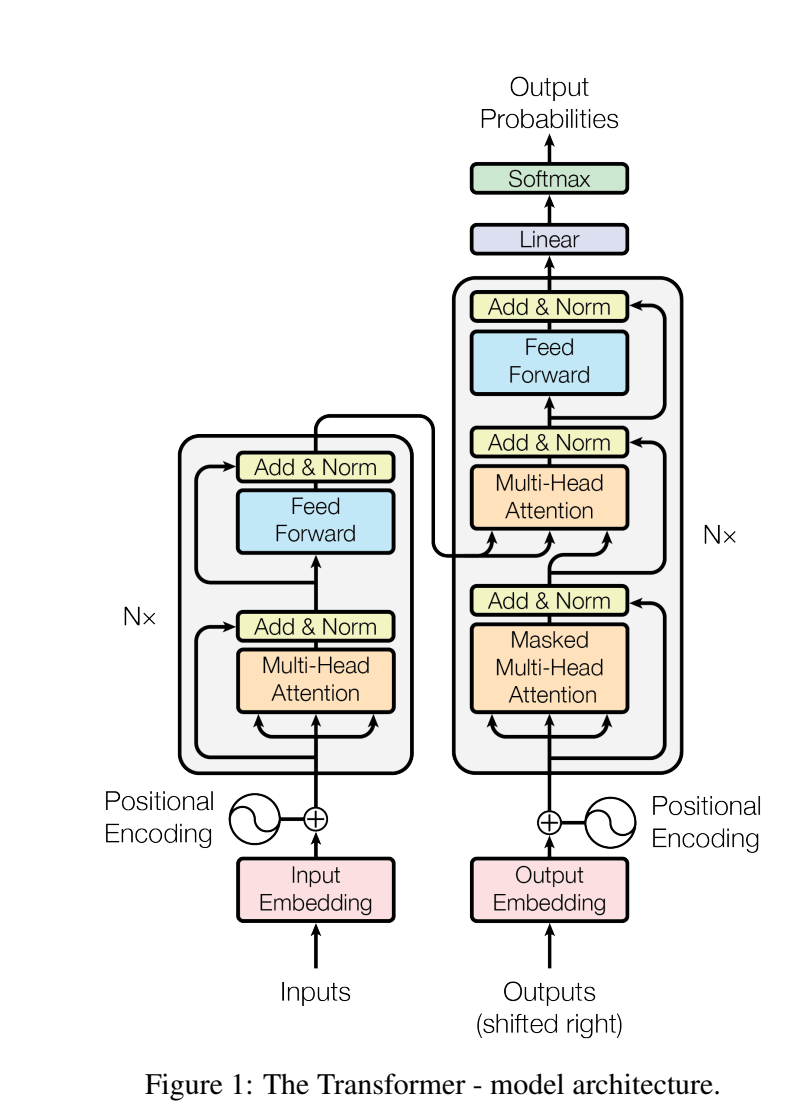
3.1. Encoder and Decoder Stacks
먼저 인코더입니다.
인코더의 layer는 여러개 중첩해서 사용할 수 있습니다. 본 논문에서는 N=6개의 layer를 중첩해서 사용하고 있습니다. 각각의 layer들은 2개의 sub-layer가 존재합니다. 첫번째 sub-layer는 Multi-Head Self-Attentiion Mechanism이고 두번째 sub-layer는 Position-Wise Fully Connected Feed-Forward Network입니다. 각 sub-layer 후에 residual connection을 적용하고 정규화 과정을 거칩니다.
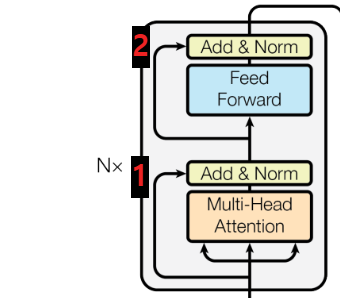
위 이미지를 보면 attention층을 지나고 Add&Norm 층에 각 sub-layer를 거치지 않은 값들이 더해지고 있습니다. 이것이 Residual Connection입니다. 기울기 소실을 예방하기 위해 Residual Connection을 사용합니다. 아래 수식과 같이 계산됩니다.
$$LayerNorm(x + Sublayer(x))$$
다음은 디코더입니다.
디코더도 인코더와 같이 여러개의 layer를 중첩해서 사용할 수 있고 본 논문에서는 N=6개의 layer를 중첩해서 사용하고 있습니다. sub-layer는 이미지에서 보이는 것과 같이 Multi-head Self-Attention Mechanism, Multi-Head Encoder-Decoder-Attention Mechanism, Position-Wise Fully Connected Feed-Forward Network 총 3개입니다.
디코더의 Self-Attention은 인코더와 달리 현재 출력 이후의 정보를 참고하지 않기 위해 뒷 부분을 Masking하여 Attention을 수행합니다.
정리하자면 Residual Connection과 Regularization을 통해 인코더와 디코더의 각 층이 안정적으로 학습되며 디코더는 마스킹을 통해 효율적인 학습을 진행합니다.
3.2. Attention
Attention 함수는 단어들 간의 관계를 나타냅니다. 이 관계를 Query와 Key-Value 쌍으로 나타낼 수 있고 수식을 통해 weighted sum으로 계산되어 하나의 Attention Value로 계산됩니다.
(사실 이 부분은 저도 잘 이해를 못하겠습니다. 머리로는 이해 하겠는데 가슴으로는 이해를 못하겠습니다.
이 부분은 여러 유튜브+블로그를 돌아다니며 이해한 내용을 합쳐놓았습니다.)
여기서 Query는 질문을 하는 주체라 할 수 있습니다. Key는 Attention을 수행할 대상이라 할 수 있습니다. 예를 들어 "사랑해"라는 단어가 생성되기 위해 "I Love You"라는 문장에 포함된 단어들 중에 어떠한 단어가 가장 중요했는지 물어보는 방식으로 각각의 Query가 Key에 대해서 Attention을 수행하는 메커니즘으로 이해할 수 있습니다. Query와 Key의 유사한 만큼의 Value를 가져온다고 합니다.
어쨌든 Q, K, V 각각의 의미가 다르게 부여되어 있는 것 같은데 저는 맘 편하게 그냥 각각 다른 신경망이 존재한다고 생각했습니다.
Q, K, V는 벡터로 이루어져있고 출력물 또한 벡터로 출력됩니다.
3.2.1 Scaled Dot-Product Attention
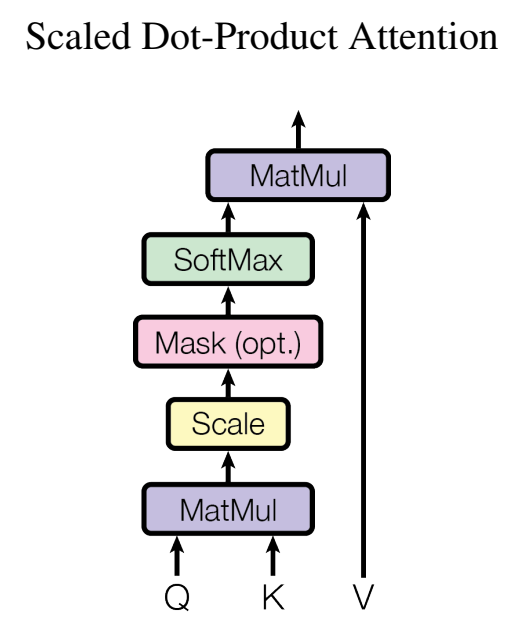
위 이미지는 하나의 Attention 메커니즘입니다. 이것이 여러개 겹쳐져 병렬적으로 수행되면 Multi-Head Attention이 되는 것입니다.
Q, K, V를 이용하여 Attention Value를 구하는 수식은 아래와 같습니다.
$$Attention(Q, K, V) = softmax(\frac {QK^T}{\sqrt{d_k}})V$$
이미지와 수식을 번갈아가며 보면 이해하기 쉽습니다.
먼저 Q와 K의 행렬곱을 수행합니다. dimension을 맞춰주기 위해 K를 Transpose하여 곱합니다. 이 결과를 Attention Score라 합니다. 그렇게 구한 Attention Score를 $\sqrt{d_k}$로 나누어 줍니다. $\sqrt{d_k}$는 이미지처럼 정규화를 위한 단계입니다. $d_k$는 Q와 K의 dimension입니다. ($d_v$는 V의 dimension입니다.)
그리고 필요하다면 Mask를 해줍니다. 디코더의 Self-Attention에서 수행되는 옵션입니다.
Softmax를 취해주고 마지막으로 V값을 곱해주면 최종 값을 구할 수 있습니다.
3.2.2 Multi-Head Attention
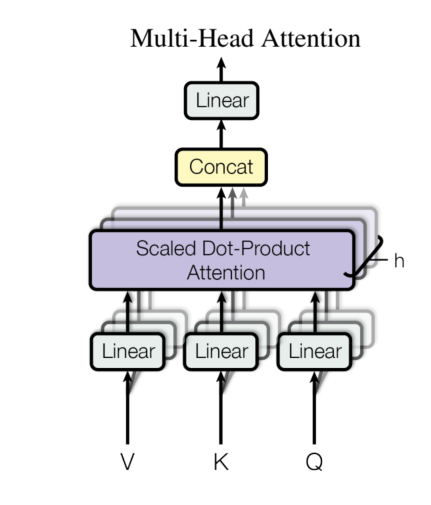
Attention을 단일로 사용하기보다 여러 개의 Attention을 병렬적으로 수행하는 것이 Multi-Head Attention입니다.
각각 다른 Q, K, V에 대해 Linear Projection을 통해 한 번에 h번의 Attention을 수행합니다. 그 결과로 $d_v$ 차원의 출력 값을 얻을 수 있습니다. 이제 이 출력 값을 병합하여 최종적으로 출력 값을 얻어낼 수 있습니다.
당연히 하나의 정보보다 여러 정보를 얻어 종합하는 것이 효과적이겠죠.
본 논문에서는 h=8의 병렬 Attention을 수행합니다. 각 h마다 $d_k = d_v = d_{model}/h = 64$로 dimension이 줄어들어 한번의 attention을 수행하나 8번의 attention을 수행하나 비슷한 computional cost을 가지게 됩니다.
3.2.3 Applications of Attention in our Model
Transformer 모델에서는 Multi-Head Attention을 세가지 방식으로 이용하고 있습니다. 1편에서 자세히 설명했지만 논문에서 언급하기에 다시 한 번 설명합니다.
- Encoder-Decoder Attention
- Q는 디코더에서 K, V는 인코더에서 가져옵니다.
- 이를 통해 현재 디코더의 position에서 모든 인코더의 모든 단어들에 관계를 파악할 수 있습니다.
- Self-Attention in Encoder
- Q, K, V가 모두 인코더 layer에서 가져옵니다. 인코더의 position에서 이전 layer의 모든 position에 대한 관계를 파악할 수 있습니다. 즉, 자기 문장에 대해 서로의 관계를 모두 파악합니다.
- Self-Attention in Decoder
- Q, K, V 모두 디코더 layer에서 가져옵니다. 방식은 Self-Attention in Encoder와 같습니다.
- 하지만 다른점은 Masking을 해준다는 점입니다. 디코더의 현재 position 이후의 정보는 Masking하여 참고하지 못하게 합니다. 즉, 현재 position 이전의 정보에만 의지하여 관계를 파악하고 학습합니다.
- Masking할 부분은 모두 음의 무한대로 설정하여 Softmax를 취하면 0에 수렴하게 합니다.
3.3 Position-wise Feed-Forward Networks
인코더와 디코더에는 fully connected feed-forward network를 포함하고 있습니다.
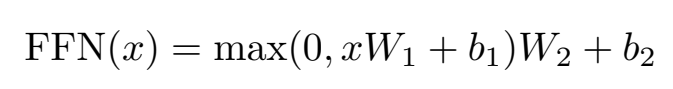
본 논문에서는 input과 output의 dimension은 512로 같습니다. 하지만 중간에 inner-layer는 2048차원으로 이루어져 있습니다.
3.4 Embeddings and Softmax
구체적인 Embedding에 대한 정보는 다루고 있지 않습니다. 기존의 모델과 비슷하다고 합니다. 우리가 알고 있는 Embedding과 Softmax를 떠올리면 될 것 같습니다.
또한 Transformer에서는 input embedding과 output embedding이 서로 가중치를 공유합니다.
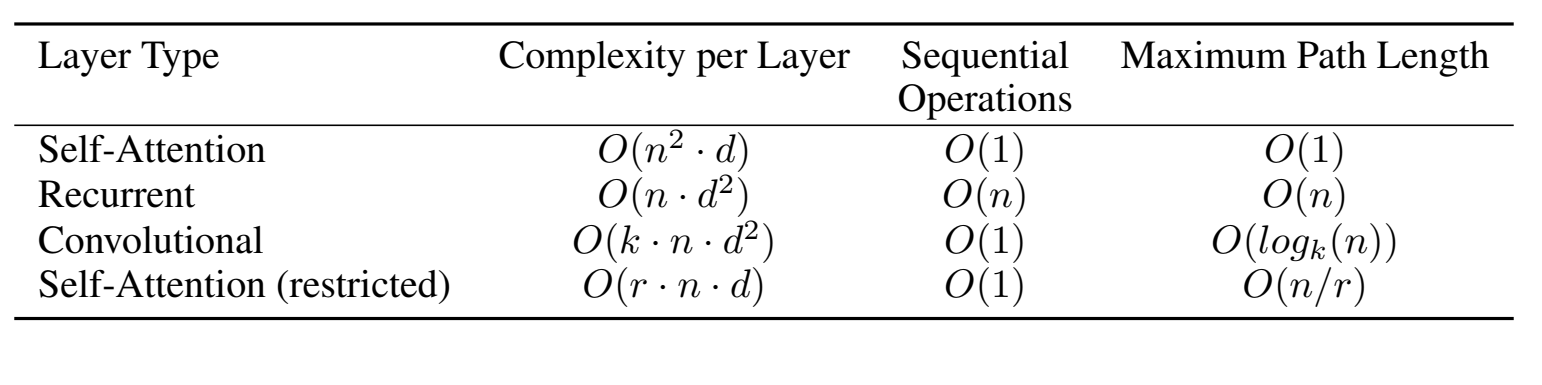
각 Layer Type에 대해 시간복잡도, 연산수, Maximum Path Length에 대해 설명하고 있습니다. Self-Attention이 기존의 방식보다 성능이 우수하다는 것을 증명하는 지표이니 간단하게 보고 넘어가도 될 것 같습니다.
3.5 Positional Encoding
Transformer 모델은 Attention mechanism만을 사용하기 때문에 순서를 알 수 없습니다. 순서에 대한 정보를 추가하기 위해 input embedding에 Positional Encoding을 더해주어야 합니다. 이를 위한 방식은 다양한데 본 논문에서는 아래와 같이 사인, 코사인 함수와 같은 주기함수를 통해 위치 정보를 추가했습니다.
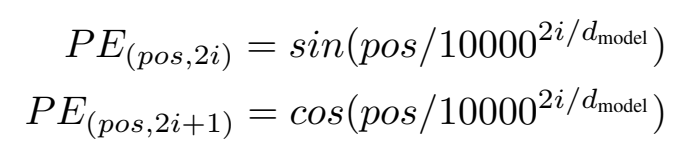
pos는 position을 나타내고 i는 dimension을 나타냅니다. 쉽게 짝수는 사인함수, 홀수는 코사인 함수를 이용합니다.
왜 주기함수를 사용했을까?? 주기함수는 최대값과 최소값이 정해져 있기 때문에 안정적입니다. 또한 주기함수이기 때문에 글자 수에 관계 없이 안정적인 값을 얻을 수 있습니다.
이러한 방법 말고도 Positional Encoding은 learned positional embeddings를 사용할 수 있습니다. 즉, 미리 학습된 모델을 통해 위치 정보를 추가하는 것입니다. 자세한 모델에 대한 설명은 없지만 성능 차이는 없다고 말하고 있습니다. 주기함수를 택한 이유는 위에서 설명했듯이 긴 시퀀스 길이 때문이라고 논문에서 설명하고 있습니다.
정말정말 중요했던 3절이 끝났습니다. 이제 4절로 넘어가겠습니다!
4. Why Self-Attention
4절에서는 왜 기존의 RNN, CNN이 아닌 Self-Attention을 선택했는지 설명합니다. 세가지 주제를 기준으로 Self-Attention의 우수성을 설명합니다. 이를 위해 3.4절의 이미지를 다시 보겠습니다.

- total computational complexity per layer (시간복잡도)
- 시퀀스 길이는 n, 차원은 d입니다. 보통은 n보다 d를 더 크게 설계하기 때문에 복잡도 면에서 Self-Attention이 가장 작은 값을 갖게 됩니다.
- amount of computation that can be parallelized (병렬화)
- 이미지의 두번째 항목을 보면 Recurrent는 n번 입력하는데 비해 Self-Attention은 단 1번의 입력만으로 처리됩니다.
- path length between long-range dependencies in the network (장거리 의존성)
- 문장이 길어질수록 거리가 먼 단어들 간의 학습에 대한 것입니다. 기존 방식들의 한계점으로 꼽히기도 합니다.
- "He is very happy because he got an A+ in exam" 문장이 있다고 가정하겠습니다.
- 한글로 번역하면 "그는 시험에서 A+를 받았기 때문에 매우 행복합니다." 입니다.
- "He is very happy because he got an A+ in exam" -> "그는 시험에서 A+를 받았기 때문에 매우 행복합니다."
- path length는 "He -> 그" 간의 거리를 말합니다.
- maximum path length는 이 중 path length가 가장 긴 것을 말합니다.
- 이 maximum path length를 줄여야 long-range dependencies를 더 잘 학습할 수 있습니다. 즉, 길이 간격이 긴 단어간의 정보를 잘 학습할 수 있는 것입니다.
- Self-Attention은 각각의 모든 단어들에 대해 직접적으로 관계를 파악하기 때문에 이 거리가 1이라고 볼 수 있습니다.
- 그러므로 Self-Attention은 긴 거리의 단어들에 대해서 더 쉽게 학습할 수 있습니다.
또한 Self-Attention은 더 설명가능한 모델을 제공합니다. Self-Attention은 각 단어를 출력할 때 어떠한 정보를 가장 많이 사용했는지 확인이 가능하기 때문에 왜 이 생성을 내놓았는지에 대한 설명이 가능합니다.
5. Training
5절은 모델의 하이퍼 파라미터나 어떠한 환경에서 실험을 진행했는지, 데이터셋은 어떠한 것을 사용했는지 등등 설명을 하고 있습니다.
6. Result
6절은 기존 모델과 Transformer의 성능 비교와 하이퍼 파라미터를 조정했을 때 생기는 차이 등을 설명하고 있습니다.
이에 대한 내용은 논문을 참고하시면 좋을 것 같습니다. 저는 바로 7절을 간단하게 요약하고 끝내보겠습니다.
7. Conclusion
본 논문은 인코더-디코더 구조에서 가장 일반적으로 사용되는 Recurrent layer를 사용하지 않고 전적으로 Attention 메커니즘에 의존하는 Transformer 모델을 제안했습니다.
실험은 영어-독일어, 영어-프랑스어 번역을 기준으로 성능을 측정했고 우수한 성능을 보였습니다. 하지만 기계번역뿐만 아니라 다양한 Task에서도 응용될 수 있음을 보였습니다.
저는 논문 리뷰에 있어서 아주아주 초짜입니다.. 그래서 알고 있던 내용임에도 불구하고 너무나 내용이 방대하고 어려웠습니다. 그만큼 얻어가는 것도 많았던 것 같습니다. 사실 저는 Transformer를 자연어 처리에서 접했는데 번역 모델인 것도 처음 알았습니다.. 모델 이름이 떡하니 Transformer인데도 말이죠..ㅋㅋ
이 논문을 처음 읽으면서 Transformer라는 모델 안에 얼마나 많은 노력과 아이디어가 들어가 있었는지 알게 되었습니다. 또한 이러한 접근법은 상상해보지도 못했기에 충격적이었던 것 같습니다.
디스커션이나 오류 지적은 항상 환영합니다 감사합니다!
+ Transformer를 이해하는데 큰 도움이 되었던 영상 몇가지를 알려드립니다.
1. 코딩오페라 (1, 2, 3강)
https://www.youtube.com/watch?v=-z2oBUZfL2o
2. 나동빈 논문 리뷰
https://www.youtube.com/watch?v=AA621UofTUA
'논문리뷰' 카테고리의 다른 글
| [논문리뷰]GPT3 - Language Models are Few-Shot Learners (0) | 2025.03.06 |
|---|---|
| [논문리뷰]Transformer: Attention Is All You Need [1] (1) | 2024.10.07 |
| [논문리뷰] Continual Learning with Deep Generative Replay (2) | 2024.10.03 |
| [논문 리뷰] Overcoming catastrophic forgetting in neural networks (0) | 2024.09.25 |
1편에 이어 작성합니다. 아래 링크를 남겨두었으니 1편을 보고 오시는 것을 추천드립니다!
https://chlduswns99.tistory.com/56
[논문리뷰]Transformer: Attention Is All You Need [1]
이번 논문은 그 유명한 Transformer입니다. Transformer는 기존의 RNN, CNN 기반 모델들에서 벗어나 오직 Attention 기법만을 이용해 설계했습니다. 현재 GPT, BERT 같은 널리 쓰이는 모델의 근간이 되는 아키
chlduswns99.tistory.com
이해를 돕기 위해 이미지를 다시 불러오겠습니다.

3.1. Encoder and Decoder Stacks
먼저 인코더입니다.
인코더의 layer는 여러개 중첩해서 사용할 수 있습니다. 본 논문에서는 N=6개의 layer를 중첩해서 사용하고 있습니다. 각각의 layer들은 2개의 sub-layer가 존재합니다. 첫번째 sub-layer는 Multi-Head Self-Attentiion Mechanism이고 두번째 sub-layer는 Position-Wise Fully Connected Feed-Forward Network입니다. 각 sub-layer 후에 residual connection을 적용하고 정규화 과정을 거칩니다.

위 이미지를 보면 attention층을 지나고 Add&Norm 층에 각 sub-layer를 거치지 않은 값들이 더해지고 있습니다. 이것이 Residual Connection입니다. 기울기 소실을 예방하기 위해 Residual Connection을 사용합니다. 아래 수식과 같이 계산됩니다.
$$LayerNorm(x + Sublayer(x))$$
다음은 디코더입니다.
디코더도 인코더와 같이 여러개의 layer를 중첩해서 사용할 수 있고 본 논문에서는 N=6개의 layer를 중첩해서 사용하고 있습니다. sub-layer는 이미지에서 보이는 것과 같이 Multi-head Self-Attention Mechanism, Multi-Head Encoder-Decoder-Attention Mechanism, Position-Wise Fully Connected Feed-Forward Network 총 3개입니다.
디코더의 Self-Attention은 인코더와 달리 현재 출력 이후의 정보를 참고하지 않기 위해 뒷 부분을 Masking하여 Attention을 수행합니다.
정리하자면 Residual Connection과 Regularization을 통해 인코더와 디코더의 각 층이 안정적으로 학습되며 디코더는 마스킹을 통해 효율적인 학습을 진행합니다.
3.2. Attention
Attention 함수는 단어들 간의 관계를 나타냅니다. 이 관계를 Query와 Key-Value 쌍으로 나타낼 수 있고 수식을 통해 weighted sum으로 계산되어 하나의 Attention Value로 계산됩니다.
(사실 이 부분은 저도 잘 이해를 못하겠습니다. 머리로는 이해 하겠는데 가슴으로는 이해를 못하겠습니다.
이 부분은 여러 유튜브+블로그를 돌아다니며 이해한 내용을 합쳐놓았습니다.)
여기서 Query는 질문을 하는 주체라 할 수 있습니다. Key는 Attention을 수행할 대상이라 할 수 있습니다. 예를 들어 "사랑해"라는 단어가 생성되기 위해 "I Love You"라는 문장에 포함된 단어들 중에 어떠한 단어가 가장 중요했는지 물어보는 방식으로 각각의 Query가 Key에 대해서 Attention을 수행하는 메커니즘으로 이해할 수 있습니다. Query와 Key의 유사한 만큼의 Value를 가져온다고 합니다.
어쨌든 Q, K, V 각각의 의미가 다르게 부여되어 있는 것 같은데 저는 맘 편하게 그냥 각각 다른 신경망이 존재한다고 생각했습니다.
Q, K, V는 벡터로 이루어져있고 출력물 또한 벡터로 출력됩니다.
3.2.1 Scaled Dot-Product Attention

위 이미지는 하나의 Attention 메커니즘입니다. 이것이 여러개 겹쳐져 병렬적으로 수행되면 Multi-Head Attention이 되는 것입니다.
Q, K, V를 이용하여 Attention Value를 구하는 수식은 아래와 같습니다.
$$Attention(Q, K, V) = softmax(\frac {QK^T}{\sqrt{d_k}})V$$
이미지와 수식을 번갈아가며 보면 이해하기 쉽습니다.
먼저 Q와 K의 행렬곱을 수행합니다. dimension을 맞춰주기 위해 K를 Transpose하여 곱합니다. 이 결과를 Attention Score라 합니다. 그렇게 구한 Attention Score를 $\sqrt{d_k}$로 나누어 줍니다. $\sqrt{d_k}$는 이미지처럼 정규화를 위한 단계입니다. $d_k$는 Q와 K의 dimension입니다. ($d_v$는 V의 dimension입니다.)
그리고 필요하다면 Mask를 해줍니다. 디코더의 Self-Attention에서 수행되는 옵션입니다.
Softmax를 취해주고 마지막으로 V값을 곱해주면 최종 값을 구할 수 있습니다.
3.2.2 Multi-Head Attention

Attention을 단일로 사용하기보다 여러 개의 Attention을 병렬적으로 수행하는 것이 Multi-Head Attention입니다.
각각 다른 Q, K, V에 대해 Linear Projection을 통해 한 번에 h번의 Attention을 수행합니다. 그 결과로 $d_v$ 차원의 출력 값을 얻을 수 있습니다. 이제 이 출력 값을 병합하여 최종적으로 출력 값을 얻어낼 수 있습니다.
당연히 하나의 정보보다 여러 정보를 얻어 종합하는 것이 효과적이겠죠.
본 논문에서는 h=8의 병렬 Attention을 수행합니다. 각 h마다 $d_k = d_v = d_{model}/h = 64$로 dimension이 줄어들어 한번의 attention을 수행하나 8번의 attention을 수행하나 비슷한 computional cost을 가지게 됩니다.
3.2.3 Applications of Attention in our Model
Transformer 모델에서는 Multi-Head Attention을 세가지 방식으로 이용하고 있습니다. 1편에서 자세히 설명했지만 논문에서 언급하기에 다시 한 번 설명합니다.
- Encoder-Decoder Attention
- Q는 디코더에서 K, V는 인코더에서 가져옵니다.
- 이를 통해 현재 디코더의 position에서 모든 인코더의 모든 단어들에 관계를 파악할 수 있습니다.
- Self-Attention in Encoder
- Q, K, V가 모두 인코더 layer에서 가져옵니다. 인코더의 position에서 이전 layer의 모든 position에 대한 관계를 파악할 수 있습니다. 즉, 자기 문장에 대해 서로의 관계를 모두 파악합니다.
- Self-Attention in Decoder
- Q, K, V 모두 디코더 layer에서 가져옵니다. 방식은 Self-Attention in Encoder와 같습니다.
- 하지만 다른점은 Masking을 해준다는 점입니다. 디코더의 현재 position 이후의 정보는 Masking하여 참고하지 못하게 합니다. 즉, 현재 position 이전의 정보에만 의지하여 관계를 파악하고 학습합니다.
- Masking할 부분은 모두 음의 무한대로 설정하여 Softmax를 취하면 0에 수렴하게 합니다.
3.3 Position-wise Feed-Forward Networks
인코더와 디코더에는 fully connected feed-forward network를 포함하고 있습니다.
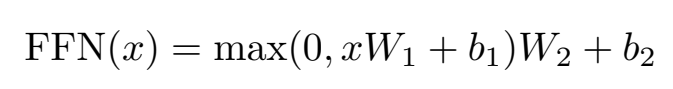
본 논문에서는 input과 output의 dimension은 512로 같습니다. 하지만 중간에 inner-layer는 2048차원으로 이루어져 있습니다.
3.4 Embeddings and Softmax
구체적인 Embedding에 대한 정보는 다루고 있지 않습니다. 기존의 모델과 비슷하다고 합니다. 우리가 알고 있는 Embedding과 Softmax를 떠올리면 될 것 같습니다.
또한 Transformer에서는 input embedding과 output embedding이 서로 가중치를 공유합니다.

각 Layer Type에 대해 시간복잡도, 연산수, Maximum Path Length에 대해 설명하고 있습니다. Self-Attention이 기존의 방식보다 성능이 우수하다는 것을 증명하는 지표이니 간단하게 보고 넘어가도 될 것 같습니다.
3.5 Positional Encoding
Transformer 모델은 Attention mechanism만을 사용하기 때문에 순서를 알 수 없습니다. 순서에 대한 정보를 추가하기 위해 input embedding에 Positional Encoding을 더해주어야 합니다. 이를 위한 방식은 다양한데 본 논문에서는 아래와 같이 사인, 코사인 함수와 같은 주기함수를 통해 위치 정보를 추가했습니다.
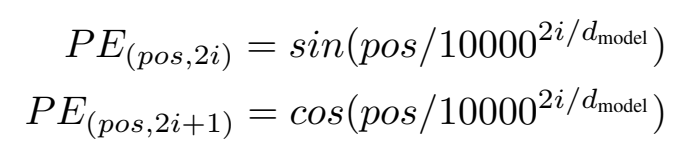
pos는 position을 나타내고 i는 dimension을 나타냅니다. 쉽게 짝수는 사인함수, 홀수는 코사인 함수를 이용합니다.
왜 주기함수를 사용했을까?? 주기함수는 최대값과 최소값이 정해져 있기 때문에 안정적입니다. 또한 주기함수이기 때문에 글자 수에 관계 없이 안정적인 값을 얻을 수 있습니다.
이러한 방법 말고도 Positional Encoding은 learned positional embeddings를 사용할 수 있습니다. 즉, 미리 학습된 모델을 통해 위치 정보를 추가하는 것입니다. 자세한 모델에 대한 설명은 없지만 성능 차이는 없다고 말하고 있습니다. 주기함수를 택한 이유는 위에서 설명했듯이 긴 시퀀스 길이 때문이라고 논문에서 설명하고 있습니다.
정말정말 중요했던 3절이 끝났습니다. 이제 4절로 넘어가겠습니다!
4. Why Self-Attention
4절에서는 왜 기존의 RNN, CNN이 아닌 Self-Attention을 선택했는지 설명합니다. 세가지 주제를 기준으로 Self-Attention의 우수성을 설명합니다. 이를 위해 3.4절의 이미지를 다시 보겠습니다.

- total computational complexity per layer (시간복잡도)
- 시퀀스 길이는 n, 차원은 d입니다. 보통은 n보다 d를 더 크게 설계하기 때문에 복잡도 면에서 Self-Attention이 가장 작은 값을 갖게 됩니다.
- amount of computation that can be parallelized (병렬화)
- 이미지의 두번째 항목을 보면 Recurrent는 n번 입력하는데 비해 Self-Attention은 단 1번의 입력만으로 처리됩니다.
- path length between long-range dependencies in the network (장거리 의존성)
- 문장이 길어질수록 거리가 먼 단어들 간의 학습에 대한 것입니다. 기존 방식들의 한계점으로 꼽히기도 합니다.
- "He is very happy because he got an A+ in exam" 문장이 있다고 가정하겠습니다.
- 한글로 번역하면 "그는 시험에서 A+를 받았기 때문에 매우 행복합니다." 입니다.
- "He is very happy because he got an A+ in exam" -> "그는 시험에서 A+를 받았기 때문에 매우 행복합니다."
- path length는 "He -> 그" 간의 거리를 말합니다.
- maximum path length는 이 중 path length가 가장 긴 것을 말합니다.
- 이 maximum path length를 줄여야 long-range dependencies를 더 잘 학습할 수 있습니다. 즉, 길이 간격이 긴 단어간의 정보를 잘 학습할 수 있는 것입니다.
- Self-Attention은 각각의 모든 단어들에 대해 직접적으로 관계를 파악하기 때문에 이 거리가 1이라고 볼 수 있습니다.
- 그러므로 Self-Attention은 긴 거리의 단어들에 대해서 더 쉽게 학습할 수 있습니다.
또한 Self-Attention은 더 설명가능한 모델을 제공합니다. Self-Attention은 각 단어를 출력할 때 어떠한 정보를 가장 많이 사용했는지 확인이 가능하기 때문에 왜 이 생성을 내놓았는지에 대한 설명이 가능합니다.
5. Training
5절은 모델의 하이퍼 파라미터나 어떠한 환경에서 실험을 진행했는지, 데이터셋은 어떠한 것을 사용했는지 등등 설명을 하고 있습니다.
6. Result
6절은 기존 모델과 Transformer의 성능 비교와 하이퍼 파라미터를 조정했을 때 생기는 차이 등을 설명하고 있습니다.
이에 대한 내용은 논문을 참고하시면 좋을 것 같습니다. 저는 바로 7절을 간단하게 요약하고 끝내보겠습니다.
7. Conclusion
본 논문은 인코더-디코더 구조에서 가장 일반적으로 사용되는 Recurrent layer를 사용하지 않고 전적으로 Attention 메커니즘에 의존하는 Transformer 모델을 제안했습니다.
실험은 영어-독일어, 영어-프랑스어 번역을 기준으로 성능을 측정했고 우수한 성능을 보였습니다. 하지만 기계번역뿐만 아니라 다양한 Task에서도 응용될 수 있음을 보였습니다.
저는 논문 리뷰에 있어서 아주아주 초짜입니다.. 그래서 알고 있던 내용임에도 불구하고 너무나 내용이 방대하고 어려웠습니다. 그만큼 얻어가는 것도 많았던 것 같습니다. 사실 저는 Transformer를 자연어 처리에서 접했는데 번역 모델인 것도 처음 알았습니다.. 모델 이름이 떡하니 Transformer인데도 말이죠..ㅋㅋ
이 논문을 처음 읽으면서 Transformer라는 모델 안에 얼마나 많은 노력과 아이디어가 들어가 있었는지 알게 되었습니다. 또한 이러한 접근법은 상상해보지도 못했기에 충격적이었던 것 같습니다.
디스커션이나 오류 지적은 항상 환영합니다 감사합니다!
+ Transformer를 이해하는데 큰 도움이 되었던 영상 몇가지를 알려드립니다.
1. 코딩오페라 (1, 2, 3강)
https://www.youtube.com/watch?v=-z2oBUZfL2o
2. 나동빈 논문 리뷰
https://www.youtube.com/watch?v=AA621UofTUA
'논문리뷰' 카테고리의 다른 글
| [논문리뷰]GPT3 - Language Models are Few-Shot Learners (0) | 2025.03.06 |
|---|---|
| [논문리뷰]Transformer: Attention Is All You Need [1] (1) | 2024.10.07 |
| [논문리뷰] Continual Learning with Deep Generative Replay (2) | 2024.10.03 |
| [논문 리뷰] Overcoming catastrophic forgetting in neural networks (0) | 2024.09.25 |
