https://www.pnas.org/doi/pdf/10.1073/pnas.1611835114
본 논문은 Catastrophic forgetting(파괴적 망각)에 대한 해결 방안을 제시하고 있습니다. 파괴적 망각에 대한 글은 아래의 제 이전 포스팅을 먼저 읽어주시면 이해에 도움이 될 것 같습니다.
https://chlduswns99.tistory.com/51
Catastrophic forgetting(파괴적 망각)이란?
Catastrophic forgetting (파괴적 망각)파괴적 망각이란 사전 학습을 마친 모델이 추가 학습을 진행할 때 이전의 지식을 잃어버리는 현상을 말합니다.즉, Task A를 학습한 모델이 Task B를 학습하면 Task A에
chlduswns99.tistory.com
Googld Deep Mind의 논문인 "Overcoming catastrophic forgetting in neural networks"은 위 포스팅에서 설명된 방법 중 Regularization-based 방식에 해당합니다. 논문에서는 Elastic Weight Consoladation (EWC) 방식을 제안했습니다.
Elastic Weight Consoladation (EWC)
- Old task를 학습한 모델이 New task를 학습할 때 가중치 변화의 정도를 제약하여 Catastrophic forgetting을 방지합니다.
- 제약을 주지 않을 경우 New task에 치우쳐져 가중치가 변화합니다. 이 경우 Ola task와 New task를 동시에 고려하지 못하게 됩니다.
- 기존의 L2 Regularization을 적용할 경우 Old task와 New task 정보를 고려하지 못해 어느 task도 적절한 결과를 얻지 못하게 됩니다.
- 빨간 화살표인 EWC 기법을 적용할 경우 Old task와 New task를 모두 고려한 공통인 부분으로 가중치가 이동하게 됩니다.
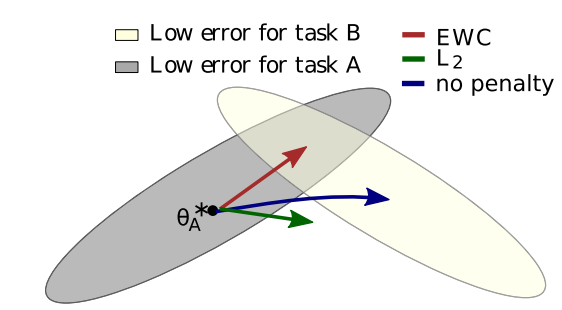
- 방식을 간단히 말하자면, ola task와 new task의 차이를 계산하여 차이가 크면 loss를 증가시키고 차이가 작으면 loss를 감소시킵니다.
- "task의 차이가 큼 -> 가중치 제약이 늘어남 -> loss 커짐"
조금 더 자세히 수식을 살펴보겠습니다.
어떤 데이터에 얼마나 제약을 줄지 결정해야 합니다. 이를 확률론적 관점에서 살펴보겠습니다.
$$ \log p(\theta|D) = \log p(D| \theta) + \log p(\theta) - \log p(D) $$
(D는 전체 데이터, $ \theta $는 가중치를 뜻합니다.)
Bayes' rule(베이즈 정리)에 log를 취하고 정리를 해주면 위와 같은 수식이 제시됩니다. Bayes' rule이란 한마디로 말하자면 이전의 경험과 현재의 조건을 토대로 어떤 사건의 확률을 추론하는 과정입니다. old task를 토대로 new task와의 관계를 증명할 수 있는 셈이죠.
- $ p(\theta) $: $ \theta $의 사전 확률
- $ p(D) $: D의 사전 확률
- $ \log p(A|B) $: 사건 B가 주어졌을 때 A의 조건부 확률
- $ \log p(\theta|D) $: 데이터 D가 주어졌을 때 $ \theta $의 조건부 확률
- $\log p(D| \theta)$: 모델의 파라미터가 $\theta$일 때 데이터 D가 관찰될 확률
우리는 데이터 D를 통해 가장 가능성이 높은 $ \theta $를 찾는 것이 최종적인 목표입니다. 결국 $ \log p(\theta|D) $ 값을 발전시켜 나가는 것이 우리의 목표입니다.
자 이제 수식을 살펴볼 준비가 끝났습니다.
위 수식을 이미 Task A가 학습된 모델에 Task B를 학습시키는 관점에서 볼 수 있게 변형시켜 보겠습니다. 위 식과 아래 식은 동일한 의미를 갖고 있습니다.
$$ \log p(\theta|D) = \log p(D_B| \theta) + \log p(\theta|D_A) - \log p(D_B) $$
- $D_B$: Task A 데이터(이전 데이터)
- $D_B$: Task B 데이터(새로운 데이터)
우리는 Task A에 대한 학습을 이미 끝냈습니다. $ \log p(\theta|D_A) $ 값을 이미 알고 있는 것입니다. 즉, $D_A$라는 데이터가 주어졌을 때 가장 최적의 $\theta$값을 알고 있는 것이죠. 그렇다면 $ \log p(\theta|D_A) $는 과거 정보를 반영한 사전 확률로서의 의미를 갖습니다. 이를 prior probability(선행확률)라 합니다.
이제 $D_B$라는 데이터가 추가로 주어졌을 때 이를 반영하여 다시 최적의 $\theta$값을 찾는 것이 목적입니다. 결과적으로 최종적으로 계산된 $\theta$는 Task A+TaskB를 모두 반영한 것입니다.
- $\log p(D_B| \theta)$: 처음 수식을 적용할 때로 보자면 $\theta$는 $D_B$에 대한 학습이 이루어지지 않았습니다. 즉, $D_A$로만 학습된 $\theta$로 $D_B$에 대한 데이터를 얼마나 잘 유추할 수 있는가? 를 보게 되는 것입니다.
- $ \log p(\theta|D_A) $: 앞서 설명했듯 학습이 완료된 $D_A$에 최적화된 $\theta$를 나타내는 것입니다. $D_B$에 대한 학습을 할 때 선행 확률의 역할을 합니다.
- $\log p(D_B)$: $\theta$에 관계없는 $D_B$가 발생할 확률을 종합한 값입니다. 최종 값을 확률로 도출하기 위해 정규화를 해야 하기 때문에 사용합니다. 결국 우리는 특정 데이터가 아닌 전체 데이터에 대해 확률을 조정해야 하기 때문이죠.
다음은 Loss function을 보겠습니다. Loss function에서 얼마나 제약을 주는지에 따라 $\theta$의 변화량이 결정될 것입니다. 즉, 새로운 데이터를 얼마나 받아들여야 이전 데이터도 잃지않고 새로운 데이터도 고려할 수 있는지 확인하는 것입니다.
수식을 보기 전에 먼저 피셔 정보 행렬에 대해 간단히 말하자면 score function의 분산을 나타냅니다. score function은 log-likelihood의 gradient를 나타냅니다. 즉, Fisher information을 이용하면 $\theta$의 중요도를 판별할 수 있습니다. $\theta$가 중요할수록 score function의 분산은 가파르게 나타납니다. 그렇다면 파라미터가 조금만 달라져도 score function이 급격하게 변하게 됩니다. 그 말은 해당 $\theta$가 성능을 결정하는 중요한 파라미터가 되는 것이죠. 정리를 해보겠습니다.
피셔정보행렬이 가파르다 -> $\theta$가 조금만 달라져도 score function이 급격하게 변한다.-> log-likelihood도 급격하게 변한다 -> 해당 $\theta$는 모델의 성능을 변화시키는 중요한 값이다. -> 그러니 $\theta$에 대한 제약을 강하게 걸어야 한다.
반대로 피셔정보행렬이 완만하다면 정확히 반대의 역할을 하게 됩니다. 자연스럽게 논문과 이어보면 old task에 중요하지 않은 파라미터라면 new task에 더 적합하게 변경시켜도 되겠다의 의미를 갖게 됩니다.
이해가 되셨다면 이제 Loss function에 대한 수식을 보겠습니다.
$$\mathcal{L}(\theta) = \mathcal{L}_B(\theta) + \sum_{i} \frac{\lambda}{2} F_i (\theta_i - \theta_{A,i}^*)^2$$
Loss를 줄이는 것이 우리의 목표입니다. 현재 Task B를 학습하고 있는 상황이기 때문에 따로 $\mathcal{L}_B(\theta)$를 계산해줍니다. 처음에는 Task B를 학습하지 않은 상황에서의 Loss를 구하는 것이겠죠.
- $\theta_i$: 현재 학습중인 $\theta_i$를 나타냅니다.
- $\theta^*_{A,i}$: Task A에 맞게 최적화된 $\theta_i$를 뜻합니다
그렇다면 $(\theta_i - \theta_{A,i}^*)^2$는 현재 학습중인 파라미터와 이전에 Task A에 맞춰진 파라미터의 차이를 나타냅니다. 즉, 이 값이 크면 현재 학습중인 파라미터가 Task A에 맞춰진 파라미터에서 많이 벗어났다는 것입니다.
다음 위에서 구한 파라미터 값을 Fisher information에 활용합니다. 피셔 정보는 위에서 설명했으니 생략하겠습니다. 이 값이 크다면 해당 파라미터는 이전 작업에서 중요한 역할을 했다는 뜻입니다. 피셔 정보가 크다면 Loss는 커집니다. 왜?? 이전 작업에서 중요한 역할을 했으니 이 파라미터는 크게 변화해선 안된다!! 라는 뜻을 가지고 있기 때문입니다.
이제 EWC 기법의 성능을 한 번 보겠습니다.
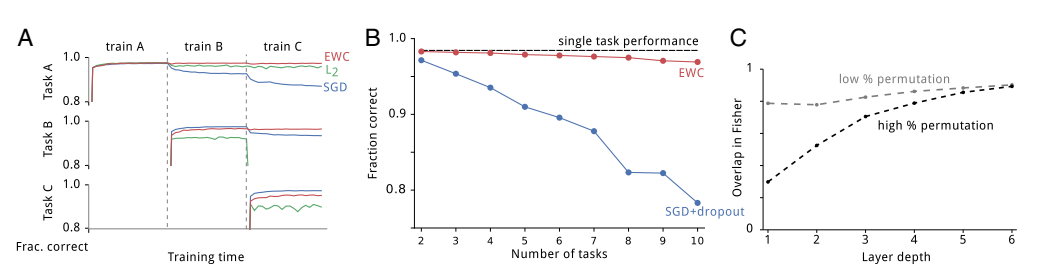
그래프 A를 먼저 보겠습니다.
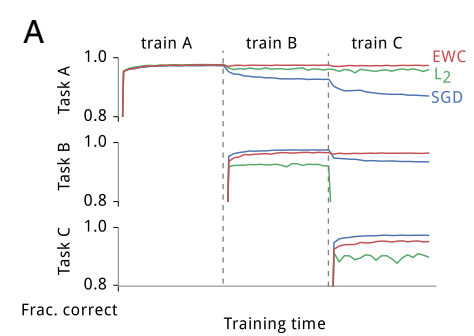
- task A만을 학습했을 때 EWC, L2, SGD 모두 비슷한 성능을 보입니다. 하지만 추가로 task B를 학습했을 때 EWC 기법이 가장 task A에 대한 성능을 잘 유지하고 있습니다. SGD랑 L2는 성능이 많이 저하되는 것을 볼 수 있습니다.
- 하지만 task A+B를 학습하고 task B에 대한 성능을 체크해보면 EWC가 SGD보다 조금 낮은 성능을 보입니다.
- 마찬가지로 task A+B+C를 학습하고 task C에 대한 성능을 체크해보면 SGD의 성능이 더 좋은 것을 볼 수 있습니다.
어쩔 수 없는 결과라고 생각합니다. 모든 태스크에 대한 성능을 유지하기 위해 단 하나의 태스크에 몰빵한 모델을 이길 수 없는 것이죠..
그다음 그래프 B를 보겠습니다.
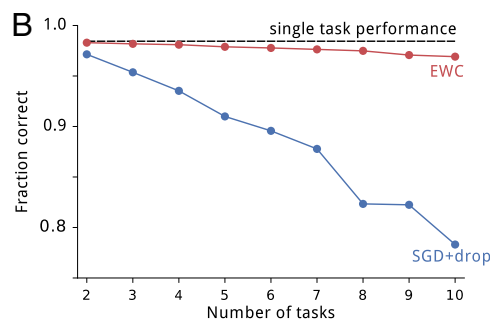
- task 10개를 학습시켰을 때의 각 task에 대한 성능을 테스트한 것입니다. EWC 기법같은 경우 10개의 task를 학습해도 거뜬하게 성능을 유지합니다. SGD+dropout 기법은 바닥을 치고 있습니다.
마지막으로 그래프 C를 보겠습니다.
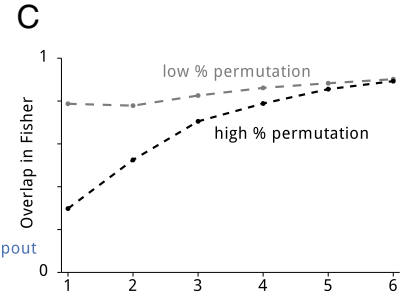
- 피셔정보에 관한 그래프인데 Overlap이 크면 두 task 간의 가중치가 서로에게 영향을 많이 주고 있다는 뜻입니다. Overlap이 낮으면 단일 task에 더 치우쳐져 있다는 것이죠.
- low permutation은 변형이 적은 순열이라는 뜻입니다. 데이터 간의 변형이 적다는 뜻입니다. 논문에서는 MNIST 데이터를 중앙의 8x8만 사용했습니다.
- high permutation은 MNIST 데이터를 28x28 모두 사용했습니다.
- 초반 Layer에서는 low permutation이 더 Overlap이 일어나지만 Layer가 깊어질수록 동일한 성능을 보이고 있습니다. 즉, 입력 패턴이 많이 다르더라도 Layer가 깊어질수록 좋은 성능을 보이고 있다는 뜻입니다.
결론
EWC 기법은 여타 다른 Regularization-based 방식에 비해 아주 높은 성능을 보이고 있습니다. 여러 태스크를 학습해도 망각 현상이 현저하게 줄어들고 있습니다. 입력 패턴이 복잡해도 Layer가 깊어질수록 low permutation과 동일한 성능을 보이고 있습니다.
제가 직접 논문을 읽고 정리된 것들을 보며 제 나름대로의 생각과 이해 방법들을 정리한 것입니다. 학문적 오류가 많을 수 있으니 지적 해주시면 감사하겠습니다.
'논문리뷰' 카테고리의 다른 글
| [논문리뷰]GPT3 - Language Models are Few-Shot Learners (0) | 2025.03.06 |
|---|---|
| [논문리뷰]Transformer: Attention Is All You Need [2] (1) | 2024.10.07 |
| [논문리뷰]Transformer: Attention Is All You Need [1] (1) | 2024.10.07 |
| [논문리뷰] Continual Learning with Deep Generative Replay (2) | 2024.10.03 |
