이번 논문도 파괴적 망각이라 불리는 Catastrophic forgetting에 관련된 논문입니다. 이에 대한 내용은 아래 포스팅을 참고해 주세요!
https://chlduswns99.tistory.com/51
Catastrophic forgetting(파괴적 망각)이란?
Catastrophic forgetting (파괴적 망각)파괴적 망각이란 사전 학습을 마친 모델이 추가 학습을 진행할 때 이전의 지식을 잃어버리는 현상을 말합니다.즉, Task A를 학습한 모델이 Task B를 학습하면 Task A에
chlduswns99.tistory.com
Abstract & Introduction 요약 및 정리
파괴적 망각을 해결하기 위해 본 논문에서는 DGR 기법을 제안했습니다. 기존의 Replay-based 방식은 이전 데이터를 별도의 메모리 공간에 저장하고 추가 학습 시 이를 포함하여 학습을 진행합니다. 이러한 방법은 큰 메모리를 필요로 하는 단점이 있습니다. 또한 real world에서 과거 기억에 직접적으로 접근한다는 것은 꽤나 비현실적입니다.
이러한 단점을 보완하고 뇌의 해마를 모방해서 만든 기법이 바로 DGR 기법입니다. 해마는 단기기억을 저장하고 있습니다. 수면중, 무의식적, 회상 등의 상황에 따라 여러 번 활성화되는 기억은 대뇌피질에서 통합되어 장기기억으로 축적됩니다. 이와 같은 시스템에 영감을 받아 DGR 기법에서는 해마와 대뇌피질의 역할을 생성 모델인 Generator와 해결 모델인 Solver로 구현했습니다.
해마는 기억을 100% 똑같이 활성화하지 않습니다. 특정 기억과 같이 활성화되거나 몇 번의 재활성화가 되는 경우 기억에 변화가 생길 수 있습니다. 이러한 해마의 특성은 별도의 메모리를 이용하여 직접적으로 데이터를 불러오는 기법보다 생성 모델을 이용하는 것이 더 합리적입니다.
GAN 기반으로 task에 맞게 훈련된 Generator를 통해 pseudo-data를 생성합니다. pseudo-data는 generator가 생성한 유사 가짜 데이터입니다. pseudo-data를 통해 solver가 response를 생성합니다. 이렇게 해서 생성된 유사 입력-출력 데이터는 과거 데이터를 재현하는 역할을 합니다. 이 generator-solver 쌍을 Scholar 모델이라 부릅니다. new task를 학습하면 새로운 데이터와 과거 데이터를 모방한 유사 데이터를 같이 학습하여 모델을 업데이트합니다. 이 과정에서 old task에 대한 정보를 유지합니다.
DGR 기법은 과거 데이터를 직접 저장하지 않고도 성능을 유지할 수 있기 때문에 개인정보를 저장하거나 재사용할 필요가 없어 개인정보 문제가 있는 실제 상황에서도 사용이 가능합니다. 또한 GAN 모델은 이미지 생성뿐만 아니라 여러 도메인에서도 데이터 분포를 재구성할 수 있기 때문에 응용 범위가 넓습니다.
여기까지가 Abstract와 Introduction에 대한 요약과 설명입니다. 이제 DGR 기법에 대해 더 자세히 알아보겠습니다.
GAN의 기본 구조
먼저 GAN의 기본 구조에 대해 알아보겠습니다.
GAN 프레임워크는 생성기(G)와 판별기(D) 사이의 제로섬 게임을 통해 훈련합니다. 생성기는 가짜 데이터를 생성하고 판별기는 데이터가 가짜인지 진짜인지 판별합니다. 이를 통해 생성기는 더욱 진짜와 유사한 데이터를 생성하고 판별기는 정교한 판별이 가능하게 됩니다. 최종적으로 생성기는 진짜와 구분이 안가는 진짜 같은 데이터를 생성하게 됩니다.
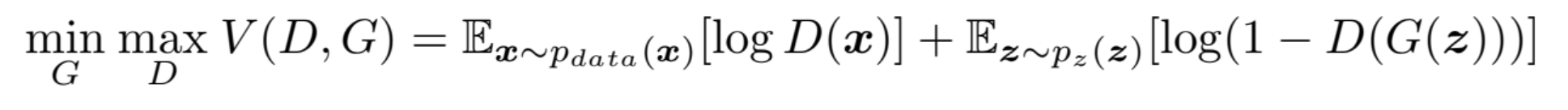
$\min_{G} \max_{D} V(D, G)$
- $\min_{G}$: 생성기는 V(G, D)를 최소화하여 판별기를 혼란에 빠뜨리려고 합니다.
- $\max_{D}$: 판별기는 V(G, D)를 최대화하여 진짜 데이터를 정확하게 예측하려 합니다.
- V(G, D): 생성기와 판별기가 경쟁하는 과정에서 각자의 목표를 표현하는 가치 함수입니다. 생성기는 판별기를 잘 속이는 것이 목표입니다. 반대로 판별기는 진짜 데이터를 잘 분류하는 것이 목표입니다.
$ \mathbb{E}_{x \sim p_{\text{data}}(x)} \left[\log D(x)\right] $
- ${x \sim p_{\text{data}}(x)}$: 진짜 데이터 x를 의미합니다. 이 데이터는 실제 데이터셋에서 온 샘플입니다.
- $\mathbb{E}_{x \sim p_{\text{data}}(x)}$: 진짜 데이터 전체에 대한 기대값(평균)을 의미합니다.
- $\log D(x)$: 판별기(D)는 진짜 데이터 x에 대해 진짜일 확률 D(x)를 출력합니다. 판별기는 진짜일수록 높은 값을 출력합니다.
정리하자면 진짜 데이터 x에 대해 판별기가 진짜라고 인식할 확률을 최대화하려는 항입니다.
$\mathbb{E}_{z \sim p_{z}(z)} \left[\log \left(1 - D(G(z))\right)\right]$
- $ {z \sim p_{z}(z)} $: 노이즈 데이터 z의 전체입니다.
- G(z): 노이즈 z를 입력받아 생성기가 가짜 데이터 G(z)를 생성합니다.
- D(G(z)): 판별기는 생성기가 만든 가짜 데이터 G(z)가 진짜일 확률을 예측합니다. 즉 값이 높을수록 생성기의 성능은 좋고 판별기의 성능이 떨어짐을 의미합니다.
- $\log (1-D(G(z)))$: 판별기가 G(z)를 가짜라고 판단한 정도를 나타냅니다. 이 값이 높을수록 판별기의 성능이 좋습니다. 그러므로 생성기의 목표는 이 값을 최소화하는 것이겠죠.
- 즉, 이 항의 의미는 모든 노이즈 데이터 z에 대해 $\log (1-D(G(z)))$의 기대값을 의미합니다.
정리하자면 가짜 데이터 G(z)에 대해 판별기가 가짜라고 인식할 확률을 최대화하려는 항입니다.
이제 각 항의 의미를 살펴보았으니 생성기와 판별기의 입장에서 이 식을 이해해 보겠습니다.
먼저 판별기의 입장에서 살펴보겠습니다. 판별기의 성능이 매우 좋아 모든 구별을 정확히 한다고 가정했을 때 D(x)는 1이 됩니다. 첫번째 항은 $log 1$이므로 0이 되는 것이 가장 이상적입니다. 두번째 항을 보겠습니다. D(G(z))는 가짜를 진짜로 인식할 확률이기 때문에 0이 될 것입니다. 즉, 1-D(G(z))는 1이 될것이고 $\log (1-D(G(z)))$는 0이 되는 것이 가장 이상적입니다. 정리해보면 판별기의 성능이 최대일 경우 수식 값이 0이 됩니다.
다음 생성기의 입장에서 살펴보겠습니다. 생성기의 성능이 매우 좋아 판별기가 모든 가짜 데이터를 부정확하게 판단한다고 가정했을 때 첫번째 항은 생성기가 관여할 수 없기 때문에 넘어가겠습니다. 두번째 항을 보면 D(G(z))가 1이 됩니다. 1-D(G(z))는 0이 될 것이고 $\log (1-D(G(z))) = \log 0$이 되므로 음의 무한대로 수렴합니다. 정리해보면 생성기의 성능이 최대일 경우 수식 값이 음의 무한대로 수렴합니다.
생성기는 값을 최소화하려 할 것이고 판별기는 값을 최대화하려 할 것입니다. 이 경쟁을 통해 생성기와 판별기의 성능을 점점 향상시키게 됩니다. 이를 적대적 학습이라 부르며 GAN의 핵심 개념이라고 할 수 있습니다.
자 이제 다시 DGR 기법으로 돌아와봅시다.
Generative Replay
먼저 몇가지 용어를 정의합니다. 학습해야 할 task를 T라하며 N개의 tasks를 $T = (T_1, T_2, \cdot\cdot\cdot, T_n)$로 정의합니다.
- Definition 1: Task $T_i$는 데이터 분포 $D_i$에서 training examples $(x_i, y_i)$를 추출하여 모델을 최적화하는 것을 목표로 합니다.
- Definition 2: scholar H는 tuple 형태인 (G, S) 한 쌍으로 정의되며 generator G는 real-like 샘플을 만들어내는 생성 모델이고 solver S는 파라미터 $\theta$로 표현되는 task solving 모델입니다.
새로운 작업을 학습하고 다른 네트워크에 자신의 지식을 가르칠 수 있는 능력을 가졌기 때문에 scholar라 부릅니다.
solver S는 task sequence T를 수행해야 합니다. 전체 목표는 전체 task간의 unbiased sum of losses를 최소화하는 것입니다. 즉, 여러 task에 대해 학습할 때 하나의 task에 편향되지 않고 모든 task에 대해 공평하게 성능을 최적화한다는 뜻입니다.
Proposed Method
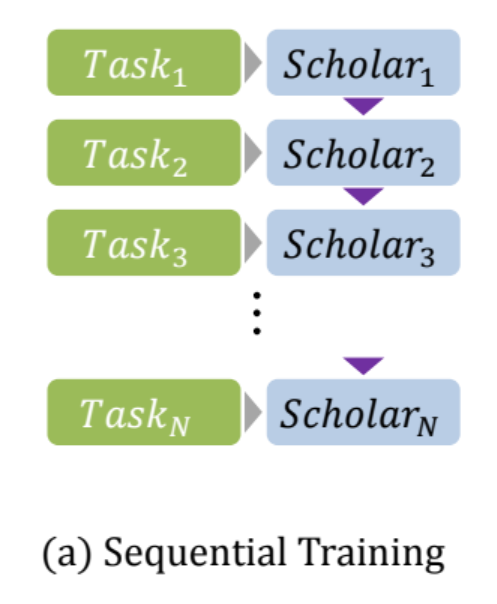
- Task마다 각자의 Scholar가 존재합니다. 위에서 설명했 듯 Scholar는 Generator와 Solver의 쌍으로 이루어져 있습니다. GAN의 구조를 따르며 Generator-Discriminator의 관계로 볼 수 있습니다.
- $(H_i)_{i=1}^{N}$는 task i=1 ~ n까지의 학습 과정을 나타냅니다. 그렇다면 $H_n$은 $T_n$과 이전 $H_{n-1}$의 지식을 가지고 있습니다.
예를 들어 Task 3에서 Scholar 3은 Scholar 1+2의 지식도 학습한 상태인 것입니다.
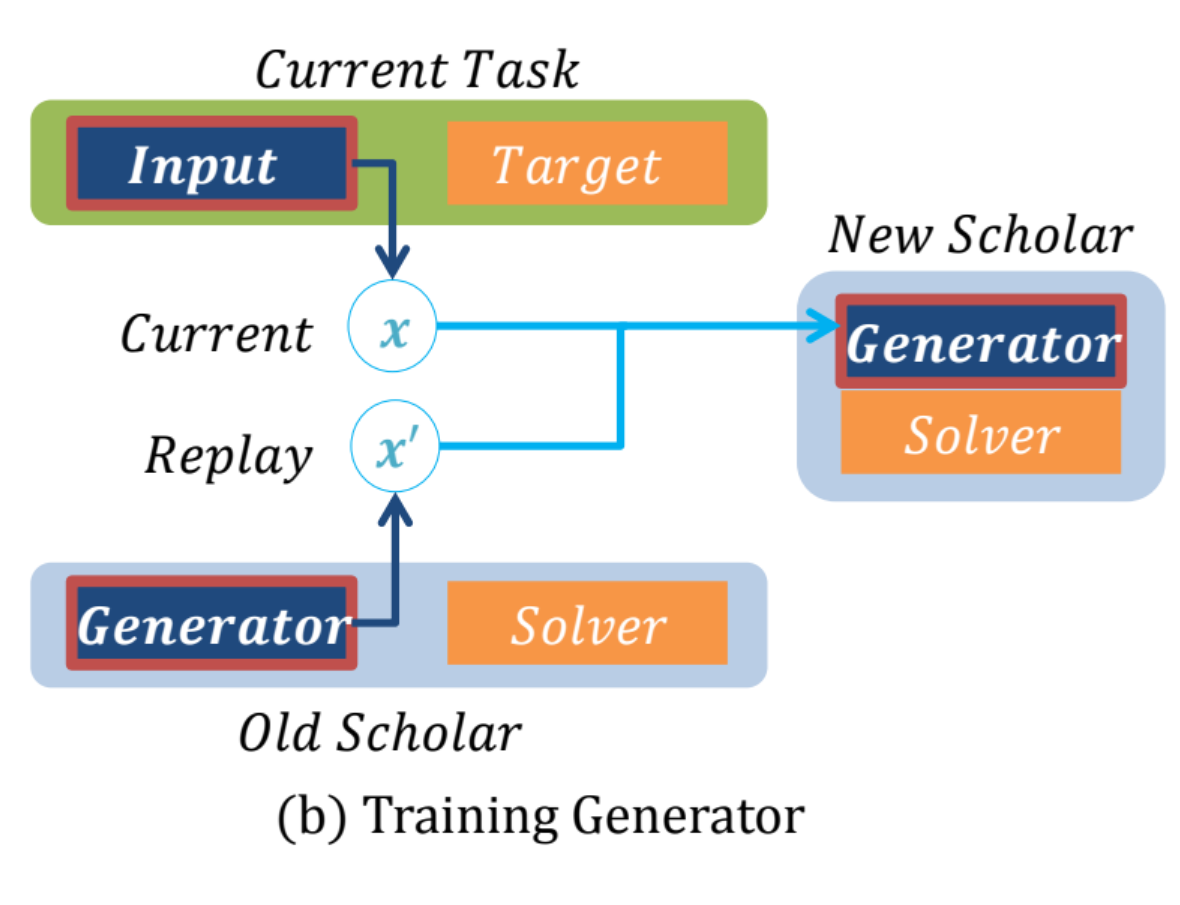
그림 (b)는 generator의 학습 과정을 나타냅니다.
(current task는 new task라 칭하겠습니다.)
- x는 new task에서의 학습 데이터입니다.
- x'는 old task에서의 학습 데이터입니다.
- new Scholar는 old task+new tesk를 섞은 데이터를 생성하도록 학습됩니다.
- 혼합 비율은 old task와 비교해 new task가 얼마나 중요한지 계산해 적절한 비율로 혼합됩니다.
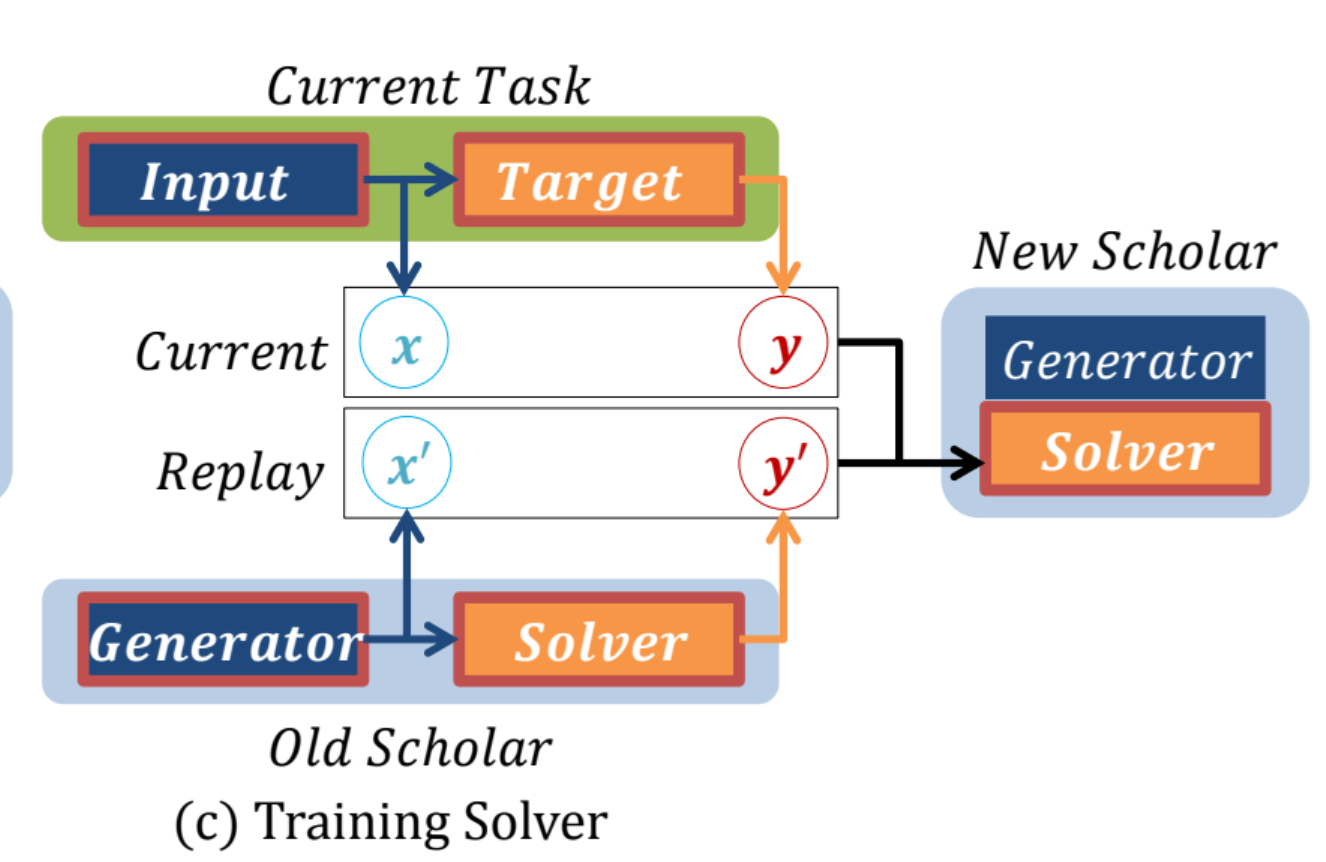
그림 (c)는 solver의 학습 과정입니다.
- generator와 학습 방법이 비슷합니다.
- new task의 실제 (x, y)와 old task의 생성된 (x', y')를 학습합니다.
- x는 input이고 y는 그에 대한 label입니다.
- 그렇다면 x'는 old generator의 generated data이고 y'는 old solver가 예측한 예측값이 될것입니다.
아래 수식은 i번째 solver의 train loss function입니다. (test loss는 조금 다릅니다.)
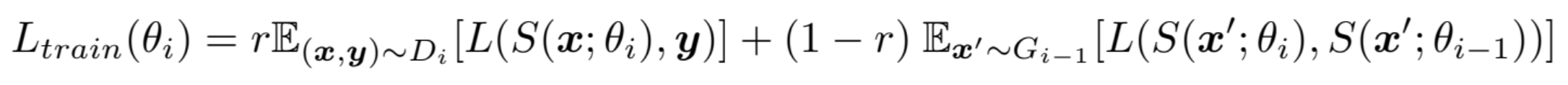
간단하게 용어 설명을 먼저 하겠습니다.
- $\theta_i$는 i번째 scholar의 파라미터입니다.
- r은 real data의 혼합 비율입니다. 그렇다면 반대로 (1-r)은 generated data의 비율입니다.
- (x, y) ~ $D_i$는 $T_i$의 데이터셋인 $D_i$의 (x, y) 데이터 쌍입니다.
- x' ~ $G_{i-1}$는 $T_{i-1}$의 generated data입니다. 즉, 가짜 데이터 x'의 전부를 의미합니다.
첫번째 항을 먼저 보겠습니다. $T_i$의 (x, y) ~ $D_i$에 대해 solver가 x를 보고 y를 예측했을 때의 Loss를 뜻합니다. 즉, solver가 얼마나 데이터를 잘 맞추었는지에 대한 Loss입니다.
두번째 항을 보겠습니다. generated data에 대해 new solver와 old solver의 예측값 사이의 Loss입니다. 이전 작업에서 학습한 지식을 유지하기 위해 old solver와 new solver의 Loss를 줄여야 합니다.
아래 수식은 test loss function입니다.
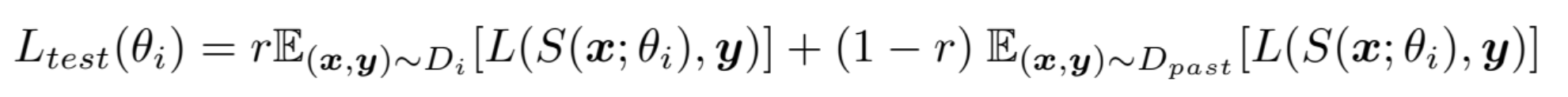
test loss는 마지막으로 학습한 $T_i$의 solver만으로 과거의 모든 task에 대한 Loss를 계산합니다. $D_{past}$는 과거의 모든 데이터를 말합니다. 예를 들어 task가 10개이고 현재 마지막 task를 학습중이라면 $D_{past}$는 task 1~9까지의 데이터를 의미합니다.
첫번째 항은 train loss와 동일합니다.
두번째 항은 train loss와는 조금 다릅니다. test loss에서는 실제 데이터에 대해 성능을 평가하기 때문에 generated data에 대한 평가가 전혀 존재하지 않습니다. 또한 두번째 항은 모든 이전 데이터에 대해 solver의 loss를 계산합니다. 이전 task의 지식들을 얼마나 잘 유지하고 있는지 평가하기 위함입니다. 당연히 i=1일 때는 두번째 항은 무시됩니다. 이전 데이터가 없기 때문입니다.
Preliminary Experiment

학습된 scholar만으로도 빈 신경망을 훈련시키기에 충분하다는 것을 입증하기 위해 MNIST 데이터셋을 이용했습니다. DGR 기법을 통해 scholar를 훈련하였으며 아래 결과는 scholar 모델이 모든 task에 대한 정보를 잃지 않았음을 증명합니다.
Solver 1은 실제 데이터를 통해 학습되었고 그 이후의 Solver들은 이전 Scholar network를 통해 학습되었습니다.
Experiment
본 실험은 다양한 DGR 기법이 여러 sequential learning settings에서 응용될 수 있음을 보여줍니다. DGR 기법을 적용한 Scholar 모델은 다른 continual learning 접근법에 비해 우수한데 그 이유는 generative model의 품질만이 성능의 제약이 되기 때문입니다. 즉, generative model이 완벽하다면 DGR 기법은 전체 데이터에셋을 한 번 학습을 한 것과 동일한 결과를 낼 수 있습니다. 이를 위해 generative model은 WGAN-GP 기법을 사용해 학습했습니다. WGAN-GP는 GAN의 개선된 기법이라고 보시면 됩니다. 본 논문에서 중요한 내용은 아니니 넘어가겠습니다.
Learning independent tasks (MNIST pixel permutation)
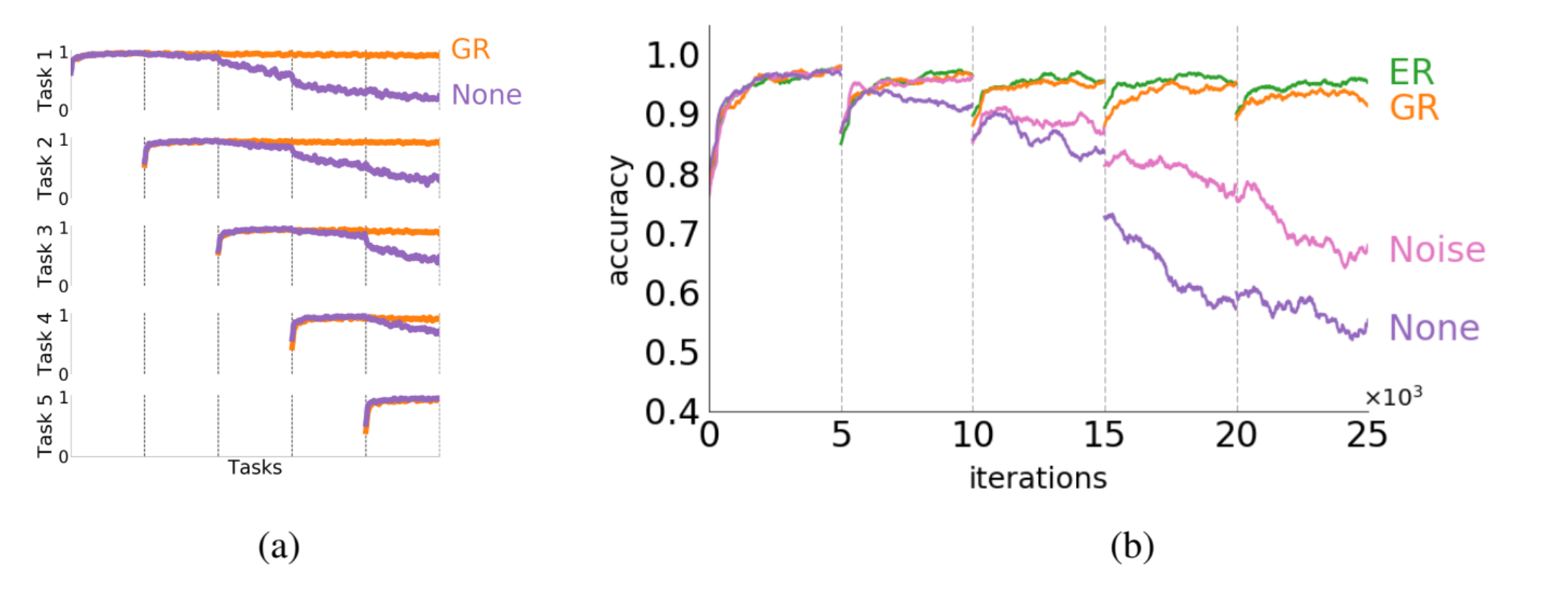
- GR: Generative Replay. 본 논문의 DGR 기법을 적용한 것입니다.
- ER: Exact Replay. 기존의 memory-replay 기법입니다. 실제 과거 데이터를 이용합니다.
- None: Naively trained solver network. 일반적으로 학습된 solver 네트워크입니다.
- Noise: generator가 데이터를 학습하지 못해 실제 데이터와 유사하지 않은 noise 데이터를 생성하는 경우입니다.
(a)를 먼저 보겠습니다. GR을 사용할 경우 task가 추가되어도 성능을 유지하는 반면 None 방식의 경우 Catastrophic forgetting 현상이 일어나 task가 많아질수록 old task의 성능이 유지되지 않고 있습니다.
(b)를 보면 ER이 가장 높은 정확도를 보이고 GR도 거의 비슷한 수준의 성능을 보이고 있습니다. Noise, None은 성능을 전혀 유지하지 못합니다.
Learning new domains (MNIST, SVHN)
다음 테스트는 서로 다른 domain에 대한 성능입니다.
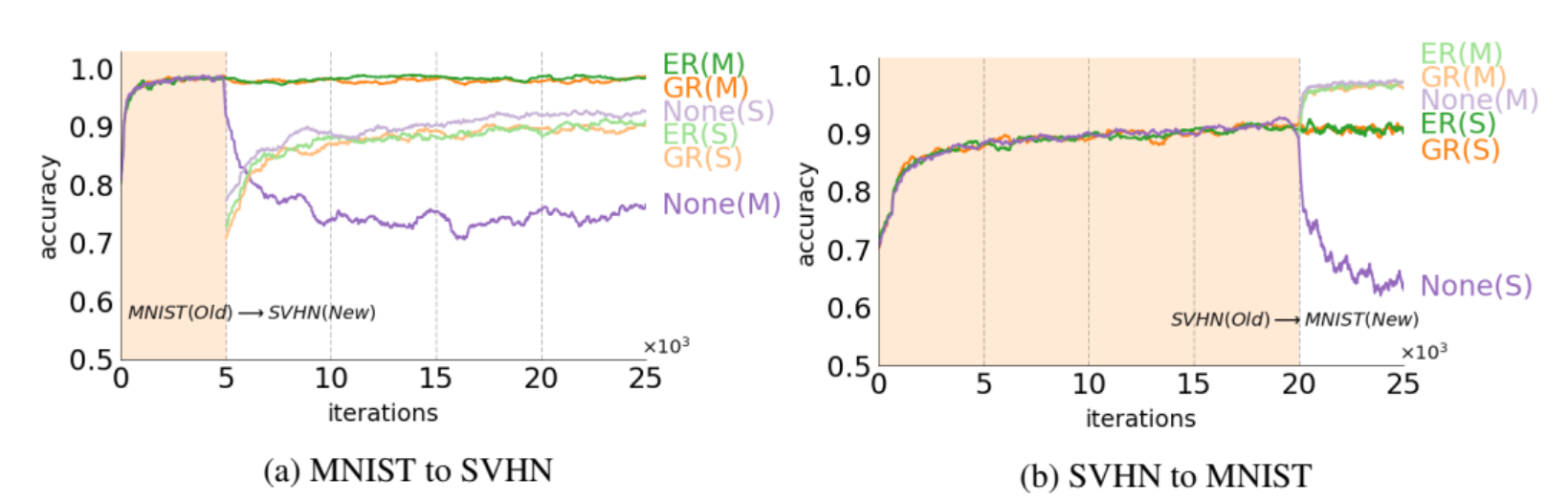
서로 다른 domain을 학습하여도 ER과 GR은 꾸준히 성능을 유지하고 있습니다. 반면 None의 경우 성능을 유지하지 못합니다.
여러 domain을 학습할 경우 categorize가 진행되며 domain간의 공유된 특성을 유추합니다.(이 부분은 정확히 이해하지 못한 것 같습니다.. 대충 서로 다른 domain에서 드러나지 않은 공통의 특성을 유추하는 것 같습니다.)
Learning new classes (MNIST)
MNIST를 여러 task로 나누어 학습한 결과입니다. 예를 들어 task1은 숫자 0, 1 데이터이고 task2는 2, 3 데이터인 경우를 의미합니다.
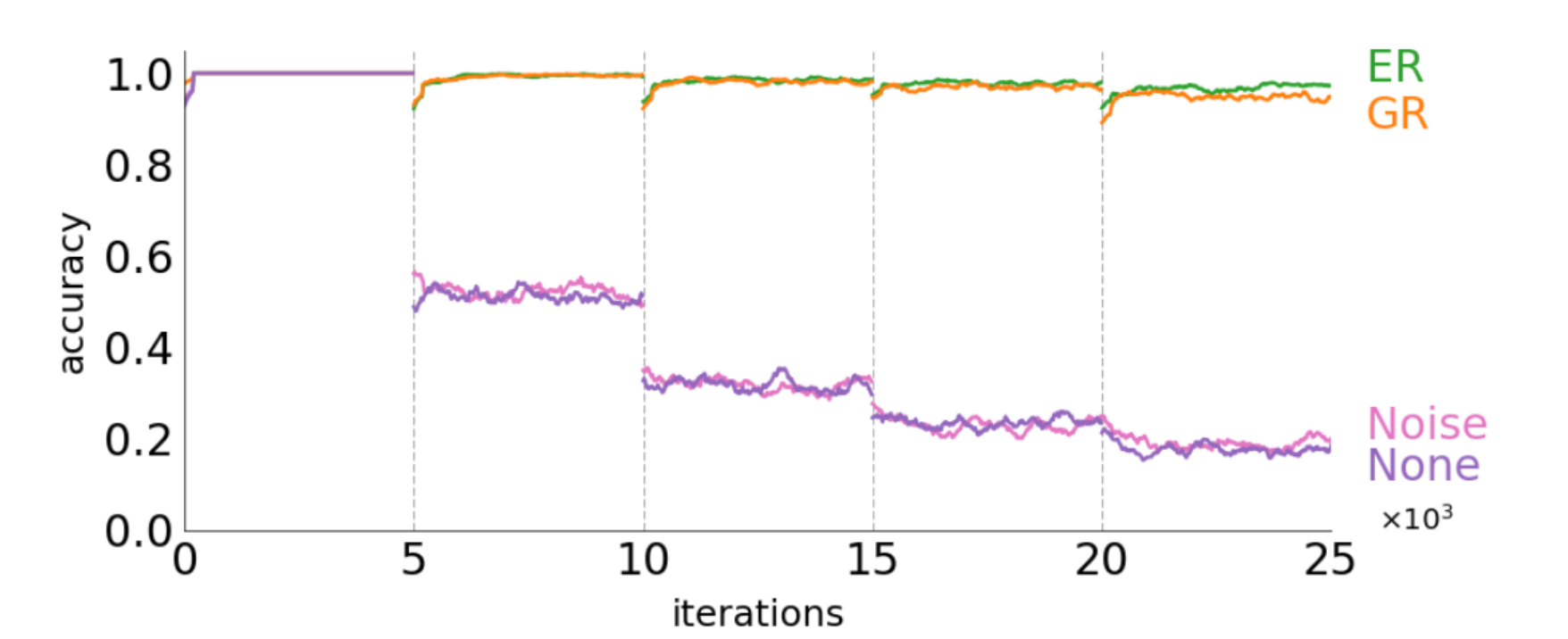
마찬가지로 ER, GR은 old task의 지식을 유지하면서 new task를 학습합니다. Noise, None은 Catastrophic forgetting 현상이 일어나면 accuracy가 급격히 저하되고 있습니다.
역시 직관적인 데이터가 존재하는 ER에 비해서는 성능이 조금 딸리는 것을 볼 수 있었습니다. 메모리 문제가 아니라면 굳이 ER을 사용하지 않을 이유가 없을 것 같습니다. 하지만 실제 해마와 대뇌피질의 작동 원리에 입각하여 설계한 기법인 것에 의의가 있다고 생각합니다.
거의 3일에 걸쳐 작성한 리뷰입니다 ..ㅠ 원론적인 개념에 입각하여 작성한 것이 아니고 이해를 기반으로 작성하여 오류가 있을 수 있습니다. 디스커션이나 오류 지적은 항상 환영입니다!!
'논문리뷰' 카테고리의 다른 글
| [논문리뷰]GPT3 - Language Models are Few-Shot Learners (0) | 2025.03.06 |
|---|---|
| [논문리뷰]Transformer: Attention Is All You Need [2] (1) | 2024.10.07 |
| [논문리뷰]Transformer: Attention Is All You Need [1] (1) | 2024.10.07 |
| [논문 리뷰] Overcoming catastrophic forgetting in neural networks (0) | 2024.09.25 |
이번 논문도 파괴적 망각이라 불리는 Catastrophic forgetting에 관련된 논문입니다. 이에 대한 내용은 아래 포스팅을 참고해 주세요!
https://chlduswns99.tistory.com/51
Catastrophic forgetting(파괴적 망각)이란?
Catastrophic forgetting (파괴적 망각)파괴적 망각이란 사전 학습을 마친 모델이 추가 학습을 진행할 때 이전의 지식을 잃어버리는 현상을 말합니다.즉, Task A를 학습한 모델이 Task B를 학습하면 Task A에
chlduswns99.tistory.com
Abstract & Introduction 요약 및 정리
파괴적 망각을 해결하기 위해 본 논문에서는 DGR 기법을 제안했습니다. 기존의 Replay-based 방식은 이전 데이터를 별도의 메모리 공간에 저장하고 추가 학습 시 이를 포함하여 학습을 진행합니다. 이러한 방법은 큰 메모리를 필요로 하는 단점이 있습니다. 또한 real world에서 과거 기억에 직접적으로 접근한다는 것은 꽤나 비현실적입니다.
이러한 단점을 보완하고 뇌의 해마를 모방해서 만든 기법이 바로 DGR 기법입니다. 해마는 단기기억을 저장하고 있습니다. 수면중, 무의식적, 회상 등의 상황에 따라 여러 번 활성화되는 기억은 대뇌피질에서 통합되어 장기기억으로 축적됩니다. 이와 같은 시스템에 영감을 받아 DGR 기법에서는 해마와 대뇌피질의 역할을 생성 모델인 Generator와 해결 모델인 Solver로 구현했습니다.
해마는 기억을 100% 똑같이 활성화하지 않습니다. 특정 기억과 같이 활성화되거나 몇 번의 재활성화가 되는 경우 기억에 변화가 생길 수 있습니다. 이러한 해마의 특성은 별도의 메모리를 이용하여 직접적으로 데이터를 불러오는 기법보다 생성 모델을 이용하는 것이 더 합리적입니다.
GAN 기반으로 task에 맞게 훈련된 Generator를 통해 pseudo-data를 생성합니다. pseudo-data는 generator가 생성한 유사 가짜 데이터입니다. pseudo-data를 통해 solver가 response를 생성합니다. 이렇게 해서 생성된 유사 입력-출력 데이터는 과거 데이터를 재현하는 역할을 합니다. 이 generator-solver 쌍을 Scholar 모델이라 부릅니다. new task를 학습하면 새로운 데이터와 과거 데이터를 모방한 유사 데이터를 같이 학습하여 모델을 업데이트합니다. 이 과정에서 old task에 대한 정보를 유지합니다.
DGR 기법은 과거 데이터를 직접 저장하지 않고도 성능을 유지할 수 있기 때문에 개인정보를 저장하거나 재사용할 필요가 없어 개인정보 문제가 있는 실제 상황에서도 사용이 가능합니다. 또한 GAN 모델은 이미지 생성뿐만 아니라 여러 도메인에서도 데이터 분포를 재구성할 수 있기 때문에 응용 범위가 넓습니다.
여기까지가 Abstract와 Introduction에 대한 요약과 설명입니다. 이제 DGR 기법에 대해 더 자세히 알아보겠습니다.
GAN의 기본 구조
먼저 GAN의 기본 구조에 대해 알아보겠습니다.
GAN 프레임워크는 생성기(G)와 판별기(D) 사이의 제로섬 게임을 통해 훈련합니다. 생성기는 가짜 데이터를 생성하고 판별기는 데이터가 가짜인지 진짜인지 판별합니다. 이를 통해 생성기는 더욱 진짜와 유사한 데이터를 생성하고 판별기는 정교한 판별이 가능하게 됩니다. 최종적으로 생성기는 진짜와 구분이 안가는 진짜 같은 데이터를 생성하게 됩니다.
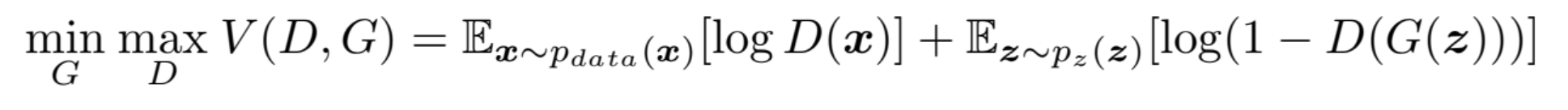
$\min_{G} \max_{D} V(D, G)$
- $\min_{G}$: 생성기는 V(G, D)를 최소화하여 판별기를 혼란에 빠뜨리려고 합니다.
- $\max_{D}$: 판별기는 V(G, D)를 최대화하여 진짜 데이터를 정확하게 예측하려 합니다.
- V(G, D): 생성기와 판별기가 경쟁하는 과정에서 각자의 목표를 표현하는 가치 함수입니다. 생성기는 판별기를 잘 속이는 것이 목표입니다. 반대로 판별기는 진짜 데이터를 잘 분류하는 것이 목표입니다.
$ \mathbb{E}_{x \sim p_{\text{data}}(x)} \left[\log D(x)\right] $
- ${x \sim p_{\text{data}}(x)}$: 진짜 데이터 x를 의미합니다. 이 데이터는 실제 데이터셋에서 온 샘플입니다.
- $\mathbb{E}_{x \sim p_{\text{data}}(x)}$: 진짜 데이터 전체에 대한 기대값(평균)을 의미합니다.
- $\log D(x)$: 판별기(D)는 진짜 데이터 x에 대해 진짜일 확률 D(x)를 출력합니다. 판별기는 진짜일수록 높은 값을 출력합니다.
정리하자면 진짜 데이터 x에 대해 판별기가 진짜라고 인식할 확률을 최대화하려는 항입니다.
$\mathbb{E}_{z \sim p_{z}(z)} \left[\log \left(1 - D(G(z))\right)\right]$
- $ {z \sim p_{z}(z)} $: 노이즈 데이터 z의 전체입니다.
- G(z): 노이즈 z를 입력받아 생성기가 가짜 데이터 G(z)를 생성합니다.
- D(G(z)): 판별기는 생성기가 만든 가짜 데이터 G(z)가 진짜일 확률을 예측합니다. 즉 값이 높을수록 생성기의 성능은 좋고 판별기의 성능이 떨어짐을 의미합니다.
- $\log (1-D(G(z)))$: 판별기가 G(z)를 가짜라고 판단한 정도를 나타냅니다. 이 값이 높을수록 판별기의 성능이 좋습니다. 그러므로 생성기의 목표는 이 값을 최소화하는 것이겠죠.
- 즉, 이 항의 의미는 모든 노이즈 데이터 z에 대해 $\log (1-D(G(z)))$의 기대값을 의미합니다.
정리하자면 가짜 데이터 G(z)에 대해 판별기가 가짜라고 인식할 확률을 최대화하려는 항입니다.
이제 각 항의 의미를 살펴보았으니 생성기와 판별기의 입장에서 이 식을 이해해 보겠습니다.
먼저 판별기의 입장에서 살펴보겠습니다. 판별기의 성능이 매우 좋아 모든 구별을 정확히 한다고 가정했을 때 D(x)는 1이 됩니다. 첫번째 항은 $log 1$이므로 0이 되는 것이 가장 이상적입니다. 두번째 항을 보겠습니다. D(G(z))는 가짜를 진짜로 인식할 확률이기 때문에 0이 될 것입니다. 즉, 1-D(G(z))는 1이 될것이고 $\log (1-D(G(z)))$는 0이 되는 것이 가장 이상적입니다. 정리해보면 판별기의 성능이 최대일 경우 수식 값이 0이 됩니다.
다음 생성기의 입장에서 살펴보겠습니다. 생성기의 성능이 매우 좋아 판별기가 모든 가짜 데이터를 부정확하게 판단한다고 가정했을 때 첫번째 항은 생성기가 관여할 수 없기 때문에 넘어가겠습니다. 두번째 항을 보면 D(G(z))가 1이 됩니다. 1-D(G(z))는 0이 될 것이고 $\log (1-D(G(z))) = \log 0$이 되므로 음의 무한대로 수렴합니다. 정리해보면 생성기의 성능이 최대일 경우 수식 값이 음의 무한대로 수렴합니다.
생성기는 값을 최소화하려 할 것이고 판별기는 값을 최대화하려 할 것입니다. 이 경쟁을 통해 생성기와 판별기의 성능을 점점 향상시키게 됩니다. 이를 적대적 학습이라 부르며 GAN의 핵심 개념이라고 할 수 있습니다.
자 이제 다시 DGR 기법으로 돌아와봅시다.
Generative Replay
먼저 몇가지 용어를 정의합니다. 학습해야 할 task를 T라하며 N개의 tasks를 $T = (T_1, T_2, \cdot\cdot\cdot, T_n)$로 정의합니다.
- Definition 1: Task $T_i$는 데이터 분포 $D_i$에서 training examples $(x_i, y_i)$를 추출하여 모델을 최적화하는 것을 목표로 합니다.
- Definition 2: scholar H는 tuple 형태인 (G, S) 한 쌍으로 정의되며 generator G는 real-like 샘플을 만들어내는 생성 모델이고 solver S는 파라미터 $\theta$로 표현되는 task solving 모델입니다.
새로운 작업을 학습하고 다른 네트워크에 자신의 지식을 가르칠 수 있는 능력을 가졌기 때문에 scholar라 부릅니다.
solver S는 task sequence T를 수행해야 합니다. 전체 목표는 전체 task간의 unbiased sum of losses를 최소화하는 것입니다. 즉, 여러 task에 대해 학습할 때 하나의 task에 편향되지 않고 모든 task에 대해 공평하게 성능을 최적화한다는 뜻입니다.
Proposed Method

- Task마다 각자의 Scholar가 존재합니다. 위에서 설명했 듯 Scholar는 Generator와 Solver의 쌍으로 이루어져 있습니다. GAN의 구조를 따르며 Generator-Discriminator의 관계로 볼 수 있습니다.
- $(H_i)_{i=1}^{N}$는 task i=1 ~ n까지의 학습 과정을 나타냅니다. 그렇다면 $H_n$은 $T_n$과 이전 $H_{n-1}$의 지식을 가지고 있습니다.
예를 들어 Task 3에서 Scholar 3은 Scholar 1+2의 지식도 학습한 상태인 것입니다.

그림 (b)는 generator의 학습 과정을 나타냅니다.
(current task는 new task라 칭하겠습니다.)
- x는 new task에서의 학습 데이터입니다.
- x'는 old task에서의 학습 데이터입니다.
- new Scholar는 old task+new tesk를 섞은 데이터를 생성하도록 학습됩니다.
- 혼합 비율은 old task와 비교해 new task가 얼마나 중요한지 계산해 적절한 비율로 혼합됩니다.

그림 (c)는 solver의 학습 과정입니다.
- generator와 학습 방법이 비슷합니다.
- new task의 실제 (x, y)와 old task의 생성된 (x', y')를 학습합니다.
- x는 input이고 y는 그에 대한 label입니다.
- 그렇다면 x'는 old generator의 generated data이고 y'는 old solver가 예측한 예측값이 될것입니다.
아래 수식은 i번째 solver의 train loss function입니다. (test loss는 조금 다릅니다.)
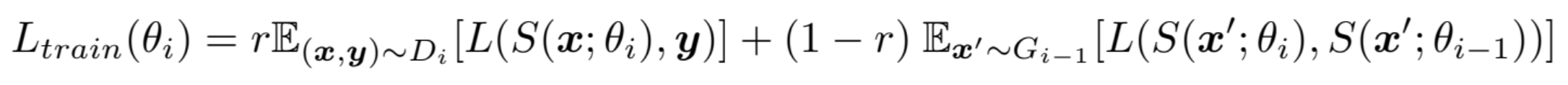
간단하게 용어 설명을 먼저 하겠습니다.
- $\theta_i$는 i번째 scholar의 파라미터입니다.
- r은 real data의 혼합 비율입니다. 그렇다면 반대로 (1-r)은 generated data의 비율입니다.
- (x, y) ~ $D_i$는 $T_i$의 데이터셋인 $D_i$의 (x, y) 데이터 쌍입니다.
- x' ~ $G_{i-1}$는 $T_{i-1}$의 generated data입니다. 즉, 가짜 데이터 x'의 전부를 의미합니다.
첫번째 항을 먼저 보겠습니다. $T_i$의 (x, y) ~ $D_i$에 대해 solver가 x를 보고 y를 예측했을 때의 Loss를 뜻합니다. 즉, solver가 얼마나 데이터를 잘 맞추었는지에 대한 Loss입니다.
두번째 항을 보겠습니다. generated data에 대해 new solver와 old solver의 예측값 사이의 Loss입니다. 이전 작업에서 학습한 지식을 유지하기 위해 old solver와 new solver의 Loss를 줄여야 합니다.
아래 수식은 test loss function입니다.
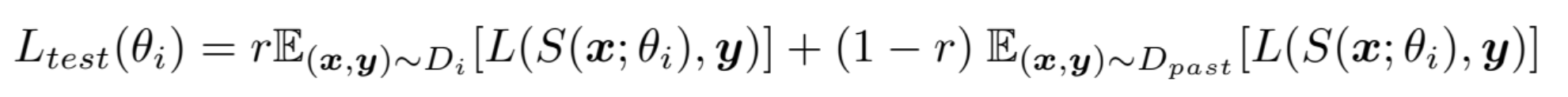
test loss는 마지막으로 학습한 $T_i$의 solver만으로 과거의 모든 task에 대한 Loss를 계산합니다. $D_{past}$는 과거의 모든 데이터를 말합니다. 예를 들어 task가 10개이고 현재 마지막 task를 학습중이라면 $D_{past}$는 task 1~9까지의 데이터를 의미합니다.
첫번째 항은 train loss와 동일합니다.
두번째 항은 train loss와는 조금 다릅니다. test loss에서는 실제 데이터에 대해 성능을 평가하기 때문에 generated data에 대한 평가가 전혀 존재하지 않습니다. 또한 두번째 항은 모든 이전 데이터에 대해 solver의 loss를 계산합니다. 이전 task의 지식들을 얼마나 잘 유지하고 있는지 평가하기 위함입니다. 당연히 i=1일 때는 두번째 항은 무시됩니다. 이전 데이터가 없기 때문입니다.
Preliminary Experiment

학습된 scholar만으로도 빈 신경망을 훈련시키기에 충분하다는 것을 입증하기 위해 MNIST 데이터셋을 이용했습니다. DGR 기법을 통해 scholar를 훈련하였으며 아래 결과는 scholar 모델이 모든 task에 대한 정보를 잃지 않았음을 증명합니다.
Solver 1은 실제 데이터를 통해 학습되었고 그 이후의 Solver들은 이전 Scholar network를 통해 학습되었습니다.
Experiment
본 실험은 다양한 DGR 기법이 여러 sequential learning settings에서 응용될 수 있음을 보여줍니다. DGR 기법을 적용한 Scholar 모델은 다른 continual learning 접근법에 비해 우수한데 그 이유는 generative model의 품질만이 성능의 제약이 되기 때문입니다. 즉, generative model이 완벽하다면 DGR 기법은 전체 데이터에셋을 한 번 학습을 한 것과 동일한 결과를 낼 수 있습니다. 이를 위해 generative model은 WGAN-GP 기법을 사용해 학습했습니다. WGAN-GP는 GAN의 개선된 기법이라고 보시면 됩니다. 본 논문에서 중요한 내용은 아니니 넘어가겠습니다.
Learning independent tasks (MNIST pixel permutation)

- GR: Generative Replay. 본 논문의 DGR 기법을 적용한 것입니다.
- ER: Exact Replay. 기존의 memory-replay 기법입니다. 실제 과거 데이터를 이용합니다.
- None: Naively trained solver network. 일반적으로 학습된 solver 네트워크입니다.
- Noise: generator가 데이터를 학습하지 못해 실제 데이터와 유사하지 않은 noise 데이터를 생성하는 경우입니다.
(a)를 먼저 보겠습니다. GR을 사용할 경우 task가 추가되어도 성능을 유지하는 반면 None 방식의 경우 Catastrophic forgetting 현상이 일어나 task가 많아질수록 old task의 성능이 유지되지 않고 있습니다.
(b)를 보면 ER이 가장 높은 정확도를 보이고 GR도 거의 비슷한 수준의 성능을 보이고 있습니다. Noise, None은 성능을 전혀 유지하지 못합니다.
Learning new domains (MNIST, SVHN)
다음 테스트는 서로 다른 domain에 대한 성능입니다.

서로 다른 domain을 학습하여도 ER과 GR은 꾸준히 성능을 유지하고 있습니다. 반면 None의 경우 성능을 유지하지 못합니다.
여러 domain을 학습할 경우 categorize가 진행되며 domain간의 공유된 특성을 유추합니다.(이 부분은 정확히 이해하지 못한 것 같습니다.. 대충 서로 다른 domain에서 드러나지 않은 공통의 특성을 유추하는 것 같습니다.)
Learning new classes (MNIST)
MNIST를 여러 task로 나누어 학습한 결과입니다. 예를 들어 task1은 숫자 0, 1 데이터이고 task2는 2, 3 데이터인 경우를 의미합니다.

마찬가지로 ER, GR은 old task의 지식을 유지하면서 new task를 학습합니다. Noise, None은 Catastrophic forgetting 현상이 일어나면 accuracy가 급격히 저하되고 있습니다.
역시 직관적인 데이터가 존재하는 ER에 비해서는 성능이 조금 딸리는 것을 볼 수 있었습니다. 메모리 문제가 아니라면 굳이 ER을 사용하지 않을 이유가 없을 것 같습니다. 하지만 실제 해마와 대뇌피질의 작동 원리에 입각하여 설계한 기법인 것에 의의가 있다고 생각합니다.
거의 3일에 걸쳐 작성한 리뷰입니다 ..ㅠ 원론적인 개념에 입각하여 작성한 것이 아니고 이해를 기반으로 작성하여 오류가 있을 수 있습니다. 디스커션이나 오류 지적은 항상 환영입니다!!
'논문리뷰' 카테고리의 다른 글
| [논문리뷰]GPT3 - Language Models are Few-Shot Learners (0) | 2025.03.06 |
|---|---|
| [논문리뷰]Transformer: Attention Is All You Need [2] (1) | 2024.10.07 |
| [논문리뷰]Transformer: Attention Is All You Need [1] (1) | 2024.10.07 |
| [논문 리뷰] Overcoming catastrophic forgetting in neural networks (0) | 2024.09.25 |
